ENGR 101 | University of Michigan

MATLAB Practice Project: Analyzing a Structure

Eigenfrequency Analysis of a Truss Bridge
Eigenfrequency Analysis of a Truss Bridge SimScale GmbH, CC BY-SA 4.0, via Wikimedia Commons

Due date: No due date, this project is always open!

Engineering intersections: Civil Engineering / Mechanical Engineering / Computer Science.

Implementing this project provides an opportunity to work with variables, matrices, indexing, functions, and unit testing in MATLAB.

This is a practice project, and your score will not affect your course grade. For this practice project, you will work with your lab group, but each student will submit their own files to the autograder. This way, everyone gets experience with submitting to the autograder and seeing how the scoring and feedback works.

Educational Objectives and Resources

This project has two aspects. First, this project is an educational tool within the context of ENGR 101, designed to help you learn certain programming skills. This project also serves as an example of a project that you might be given at an internship or job in the future; therefore, we have structured the project description in way that is similar to the kind of document you might be given in your future professional capacity.

Educational Objectives

The primary purpose of this project is to get hands-on experience working with matrices in MATLAB and manipulating data to do some kind of analysis. The secondary purpose is to reinforce why we write our own functions: because the function needs to be evaluated many times for different input values and because it can be used just like a built-in function.

Project Roadmap

This is a big picture view of how to complete this project. It’s like a table of contents. You can find many more details throughout the rest of the spec.

Submission and Grading

The deliverables for this practice project are MATLAB function files:

Submit these files to the autograder for grading.

The autograder will run a set of public tests - these are the same as the test scripts provided in this project specification. It will give you your score on these tests, as well as feedback on their output.

The autograder also runs a set of hidden tests. These are additional tests of your code (e.g. special cases). You still see your score on these tests, but you do not receive feedback on their output. The reason we do not give full feedback on all tests is because part of the project goal is for you to learn to develop effective testing practices of your own.

Your score on the public and hidden tests combined makes up your final autograder score. If you make multiple submissions, your autograder score is the best score from any submission. The submission with the best score is also the one used for style grading. If multiple submissions have the best score, we use the most recent one for style grading.

For example, let’s assume that I turned in the following:

Submission # 1 2 3 4
Score 10 35 35 20

Then my grade for the Autograded portion would be 35 points (the best score of all submissions) and Submission #3 would be style graded since it is the latest submission with the best score. Note: there is no style grading for the practice project as this project does not count towards your final grade.

Autograder Details

There are some specific details to be aware of when working with the autograder. Make sure you understand these so you will have successful submissions.

Test Case Description and Error Messages

Each of the test cases on the Autograder is testing for specific things about your code. Often, it’s checking to see if your programs can handle “special cases” of data, like if a matrix would typically have lots of different numbers in it but your function should still work correctly if the matrix is all zeroes or all negative numbers.

Each of the test cases on the Autograder has a description of what it’s checking for. Additionally, if your program fails a test case, the Autograder will give you some advice on how to go about debugging your code. It’s like you have a friendly GSI or IA giving you immediate help!

Suppressing Output

The test scripts discussed in these project specifications display output in the command window, but your function implementations for both tasks 1 and 2 should not display anything in the command window when they run. Suppress all output within functions by using semicolons, as is best practice.

Acceptable Functions

Due to the structure of the autograder, there are certain limitations on which functions you can use and how you need to use them:

If you fail to follow these guidelines, your functions will not run in the autograder.

Precision

Floating point numbers (i.e. numbers with a decimal point) can only be represented with a finite amount of precision on a computer. This means we can run into issues with roundoff error, where two different (correct) methods of computing the same result can yield numbers that are not precisely equal. Because of this, the autograder allows a certain amount of tolerance in the numeric results of your code - anything within 0.01 of the correct result will be treated as correct.

The autograder uses a custom function named almostEqual to compare the results produced by your functions to the correct answers. If you see feedback on the autograder about an almostEqual function, then that means your function is not calculating the correct return value(s).

Project Overview

Background and Motivation

It’s been two years since we established our settlement on Proxima b. We have built several domed structures to protect citizens from the harsh atmosphere, but space within the domes is extremely limited. One proposal for more efficient usage of this space is to build underground structures below existing buildings to store materials and park our fleet of autonomous rovers.

Map of pretend dome settlements on Proxima b, as named by previous ENGR 101 students. Name of domes: Dimmsdale Dimmadome, James Earl Dome, Dumbledome, Domey McDomeface. Picture of an underground parking structure.
Several domed settlements already exist. Underground structures are an efficient way to use the limited space available within the domes.

A crucial engineering challenge for underground structures is ensuring they are able to support the weight of the buildings above them. The citizens are able to manufacture metal support poles, which can be used to help hold everything up. For this project, we make a simplifying assumption that the load on the structure will be carried by four support poles placed in each quadrant of a rectangular structure (more details below).

Your Job

Your team is working to analyze the stability of an underground structure based on possible values of several design parameters (e.g. the nature of the support poles, the distribution of weight above the structure, etc.). You will implement the calculations involved in these analyses as a library of MATLAB functions. You will also use unit tests to ensure functions are working correctly.

Deliverables

The deliverables for this practice project are MATLAB function files:

Submit these files to the autograder for grading.

Starter Code and Test Scripts

The starter code files contain some code that is already written for you, and you will write the rest of the code needed to implement the tasks described in the Project Task Description section. The starter code files all have _starter appended to the file’s name so that if you want to download a fresh copy of the starter code, you won’t accidentally overwrite an existing version of the file that may have some code you have written in it. Remember to remove the _starter part of the filename so that your programs will run correctly!

Click the filenames to download the starter code:

Here are some test scripts that you can use as a base for testing your functions. Each test script includes at least one test case as an example. You should add more test cases, using the example test case(s) as a template, to verify that your functions are working correctly.

Click the filenames to download the test scripts:

Note: The UnitTests_LargestLoad.m test script is designed to be used with the lab exercises, not on its own, as you will see once you get to lab. The UnitTests_AdditionalPallets.m is a more traditional test script for a MATLAB function.

Project Task Description

Task 1: Computing the Largest Load on the Support Poles

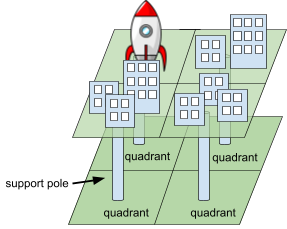
This task is to compute the largest load the support poles will need to bear. The term load refers to the force that acts along the length of the support pole. The load is based on the weight of the buildings above the structure, and we are primarily concerned with finding the single pole that bears the most weight (it would be the first to break if the load is too high for the pole to withstand).

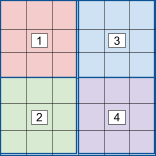
For this task, we assume the structure is rectangular in shape and that four support poles are used to hold up the “ceiling” (and the buildings on top of it). The structure is divided into four quadrants, with a support pole placed in the center of each. We assume each pole carries all of the load in its quadrant.

We will model the layout of the structure with a 2D matrix, where each element in the matrix represents a 10x10ft area on top of the structure. The value of each element in the matrix is the load applied on that portion of the underground structure, due to the weight of the buildings and/or other objects on top of the structure in that 10x10ft area.

You may assume that the matrix representing the loads on the structure can be exactly divided into four equally sized submatrices representing the four quadrants without any rows or columns overlapping.

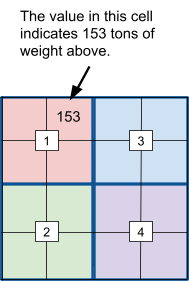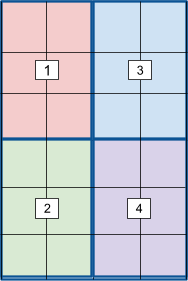A 4-by-4 matrix divided up into four 2-by-2 quadrants. Each quadrant has a support pole in the middle. A 6-by-4 matrix divided up into four 3-by-2 quadrants. Each quadrant has a support pole in the middle. A 5-by-5 matrix divided up into two 3-by-3 quadrants and two 3-by-2 quadrants. These quadrants are not all equal-sized, so this is not a valid matrix to be passed to the function.
These diagrams illustrate how the matrix of weights can be divided up into four equal-sized quadrants. The locations of the support poles is shown in the numbered boxes -- one pole in the center of each quadrant. The matrix of weights must have an even number of rows and and even number of columns; otherwise, we are not able to divide the matrix up into equal-sized quadrants.

Algorithm

For this task, write a function named largestLoad, which computes the largest load placed on any individual support pole.

Use the following algorithm to compute the largest load:

Step 1:
Use indexing to select four equally sized submatrices for each quadrant.

Step 2:
Compute the sum of the loads in each quadrant (i.e. the sum of elements in each submatrix).

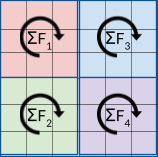
Step 3:
Determine the maximum load among the four quadrants and return that value.

Function definition and description

The function header and comments are provided for you in the file called largestLoad_starter.m. Don’t forget to remove _starter from the filename before you try to call this function.

function [maxLoad] = largestLoad(W)
% largestLoad computes the largest load any of the support poles would
% need to bear based on the distribution of forces in the W matrix. 
% We assume each pole is solely responsible for the forces in its quadrant.

% W: Weights matrix (Distribution of weight on the roof)
%      
% maxLoad: the largest load among any of the four support poles

Write your implementation of the function in this file.

Testing your largestLoad function

To test your largestLoad function, use the testing script provided with the starter files, UnitTests_LargestLoad.m. Here is an example of a test case for the largestLoad function:

W = [5, 4, 4, 3 ;
     3, 9, 8, 3 ;
     4, 2, 1, 8 ;
     3, 4, 1, 2 ];
 
result = largestLoad(W);
expected_result = 21;

% Display a nice summary of this test case in the Command Window
disp("Test 0:");
disp("Result from calling largestLoad is:");
disp(result);
disp("Expected result is:");
disp(expected_result);

If your largestLoad function is working correctly, you should get the following output when running the test script:

>> Test 0:
Result from calling largestLoad is:
    21

Expected result is:
    21

The result from calling largestLoad matches the expected result, so the function passes this test case.

Remember: The UnitTests_LargestLoad.m test script is designed to be used with the lab exercises, not on its own, as you will see once you get to lab.

We recommend you test this function thoroughly, especially to make sure it works correctly for each of the four quadrants.

Task 2: Determining Storage Capacity

A portion of the structure will be used for long-term storage of supplies (e.g. non-perishable food, medicine, old ENGR 101 exams, etc.). The supplies are packed into pallets, which are arranged into a grid; each grid space is the length and width of one pallet. The pallets can be stacked on top of each other, assuming their height does not exceed the height of the ceiling.

Assume that all pallets are exactly the same size. They have square bases and a fixed height. Pallets are stored in a rectangular grid, which we will represent with a matrix. Each cell in the matrix contains a number to indicate how many pallets are stacked there. Your task is to write a function that computes the additional number of pallets that can be stored, based on the existing pallets, the height of the storage area, and the height of each pallet.

Left: a picture of a warehouse, you can see pallets containing a variety of goods. Right: a diagram showing a matrix representing how many pallets are in each storage spot and how to calculate how many additional pallets can be stored in each space.
(Left) Supplies on pallets; pallets stacked in designated spaces in the storage facility. (Right) A diagram showing a matrix representing how many pallets are in each storage spot and how to calculate how many additional pallets can be stored in each space.

Function definition and description

The function header and comments are provided for you in a file called additionalPallets_starter.m. Don’t forget to remove _starter from the filename before you try to call this function.

function [numPallets] = additionalPallets(roofHeight, pallets, palletHeight)
% additionalPallets computes the number of additional storage pallets
% that can fit in the storage area of the structure
%
% roofHeight: scalar representing the height of the roof
%
% pallets: a matrix representing the number of pallets in 
%          each storage cell of the storage area
%
% palletHeight: scalar representing the height of a single 
%               pallet
%
% numPallets: number of additional pallets that can fit in 
%             the storage area

Write your implementation of the function in this file.

Hint: You may find the floor() function helpful.

Note: You can assume that the values in the pallets matrix will be less than or equal to the maximum number that could fit given the roof height. In other words, no storage cell will already be exceeding the capacity.

Testing your additionalPallets function

To test your additionalPallets function, use the testing script provided with the starter files, UnitTests_AdditionalPallets.m. Here is an example of a test case for the additionalPallets function:

roofHeight = 10;
pallets = [3, 2, 4;
           4, 1, 3;
           1, 4, 5];
palletHeight = 2;
 
result = additionalPallets(roofHeight, pallets, palletHeight);
expected_result = 18;

% Display a nice summary of this test case in the Command Window
disp("Test 1:");
disp("Result from calling additionalPallets is:");
disp(result);
disp("Expected result is:");
disp(expected_result);

If your additionalPallets function is working correctly, you should get the following output when running the test script:

>> >> UnitTests_AdditionalPallets
Test 1:
Result from calling additionalPallets is:
    18

Expected result is:
    18

The result from calling additionalPallets matches the expected result, so the function passes this test case.

We recommend you test this function thoroughly, especially with a variety of initial configurations and pallet heights.

Extra Practice: Computing Parking Revenue

This part is completely optional.

The underground structure will also provide parking for our fleet of rovers. To help fund ongoing maintenance of the structure, we plan to charge parking fees for each space. Your task is to compute the total amount earned in a day based on usage for each space and the fee charged (some spaces charge higher rates per hour).

The underground structure is divided into equal sized spaces, each of which has different designations: parking and storage. Parking spaces are located around the edge of the structure. We will use matrices to represent the data associated with each space (because we also rent out the storage spaces), but only the values on the edges of the matrix are relevant for the parking revenue calculation. Your code should not use values from the middle of the matrices.

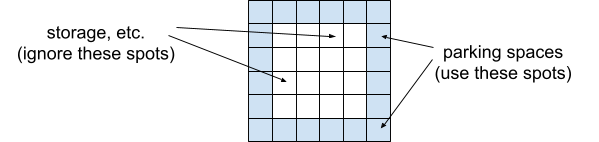A matrix representing all of the spaces that we will rent out to citizens. The storage spaces are in the middle and the parking spaces are along the edges.
A matrix representing all of the spaces that we will rent out to citizens. The storage spaces are in the middle and the parking spaces are along the edges.

You will write a function called parkingRevenue that computes the total amount earned for a particular day. The data for the number of hours each parking spot was used and the price per hour are stored in two parallel matrices.

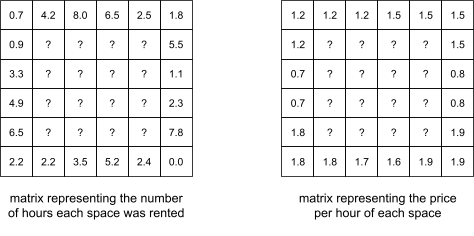Left: A matrix representing the number of hours each space was rented. Right: A matrix representing the price per hour of each space. These matrices are the same size.
Examples of data that might be passed in as parameters to the parkingRevenue function.

You may assume these matrices are the same size. Again, only the edge values in the matrix should be considered, because that is where the parking spots are located.

Function definition and description

The function header and comments are provided for you in a file called parkingRevenue_starter.m.

function [revenue] = parkingRevenue(timeUsed, price)
% parkingRevenue computes the revenue from parking fees 
%
% timeUsed: a matrix with the number of hours each spot was used
%
% price: a matrix with the price per hour for each spot
%
% ONLY THE EDGE VALUES FROM EACH MATRIX SHOULD BE USED
%     
% revenue: the total amount earned from all parking spots

Write your implementation of the function in this file.

Testing your parkingRevenue function

To test your parkingRevenue function, use the testing script UnitTests_ParkingRevenue.m.

UnitTests_ParkingRevenue.m:
timeUsed = [0.5 4.0 8.0 1.2;
            3.0 0.0 0.0 5.0;
            7.4 0.0 0.0 3.5;
            2.0 1.0 1.5 4.0];
 
price = [0.8 0.8 0.9 0.9;
         0.8 0.0 0.0 0.9;
         1.5 0.0 0.0 1.5;
         1.5 1.5 1.5 1.9];
     
result = parkingRevenue(timeUsed, price);
expected_result = 49.48;

% Display a nice summary of this test case in the Command Window
disp("Test 1:");
disp("Result from calling parkingRevenue is:");
disp(result);
disp("Expected result is:");
disp(expected_result);

If your parkingRevenue function is working correctly, you should get the following output when running the test script:

>> >> UnitTests_ParkingRevenue
Test 1:
Result from calling parkingRevenue is:
   49.4800

Expected result is:
   49.4800

The result from calling parkingRevenue matches the expected result, so the function passes this test case.

We recommend you test this function, especially with a variety of matrices (values and sizes) for the time used and the price per space.